PERBANDINGAN SEGMEN GARIS

PERBANDINGAN SEGMEN GARIS

Apakah kamu punya penggaris panjang? Penggaris mana yang kamu miliki? Penggaris berukuran 20 cm atau 30 cm? Jika belum punya, silahkan pinjam ke teman sebangku dan kumpulkan kedua penggaris itu. Jika kedua penggaris itu memiliki ukuran panjang yang berbeda, bisakah kamu menyebutkan berapa perbandingannya? Agar kamu dapat menjawabnya, yuk simak topik ini dengan saksama.

Sebelum kamu belajar tentang perbandingan segmen garis, mari kita ingat kembali definisi garis.

Garis

Suatu garis terbentuk dari hubungan antara dua titik yang tidak berhimpit dan membentuk garis lurus. Suatu garis tidak memiliki ujung atau pangkal. Jika suatu garis memiliki pangkal tapi tidak berujung, dinamakan sinar garis, sedangkan jika suatu garis memiliki pangkal dan ujung, dinamakan ruas garis. Penamaan suatu garis dapat dituliskan menggunakan huruf kecil seperti g, h, k, l dan sebagainya, sedangkan penamaan untuk ruas garis dapat dituliskan nama titik penyusunya.

Nah, sekarang kamu pasti telah ingat kembali definisi garis. Selanjutnya, mari kita belajar tentang perbandingan segmen garis.

Perbandingan Segmen Garis

Suatu garis dapat dibagi menjadi n bagian sama panjang atau dengan perbandingan tertentu. Agar lebih jelas, perhatikan gambar berikut ini.

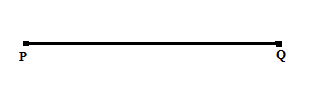
          Ruas garis PQ dan ruas garis QP adalah ruas garis yang sama karena keduanya merupakan himpunan titik-titik yang sama, sehingga dapat ditulis PQ = QP. Jika pada ruas garis PQ kita sisipkan titik O, maka terdapat 2 segmen garis yaitu PO dan OQ.

          Jika berlaku PO = OQ, maka O merupakan titik tengah ruas garis PQ dengan perbandingan PO : OQ = 1 : 1. Dengan demikian, kita telah membagi ruas garis PQ menjadi nbagian sama panjang, dengan n = 2. Kita juga dapat membagi ruas garis PQ dengan perbandingan tertentu, yaitu dengan menyisipkan titik O di antara ruas garis PQ dengan perbandingan PO : OQ sesuai dengan yang kita inginkan atau membaginya menjadi beberapa segmen garis.

Selanjutnya, perhatikan beberapa segmen garis berikut.

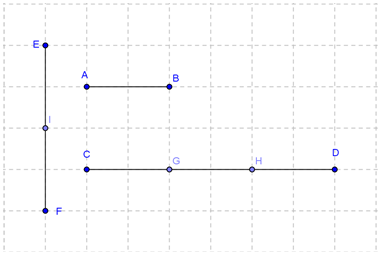
          Panjang AB = 2 satuan panjang, panjang CD = 6 satuan panjang dan panjang EF = 4 satuan panjang. Perbandingan segmen garis AB dan segmen garis CD sama dengan satu banding tiga, ditulis AB : CD = 1 : 3. Dapat juga dinyatakan dengan 3AB = CD. Perbandingan segmen garis AB dan segmen garis EF sama dengan satu banding dua, ditulis AB : EF = 1 : 2. Dapat juga dinyatakan dengan 2AB = EF. Selanjutnya, perbandingan segmen garis CG dan segmen garis CD sama dengan satu banding tiga, ditulis CG : CD = 1 : 3. Dapat juga dinyatakan dengan 3CG = CD.

Mudah sekali, kan? Agar kalian lebih paham, perhatikan contoh di bawah ini.

Contoh

Contoh 1:

Perbandingan ruas garis AB : AC = 2 : 3. Jika panjang AB = 4 cm, maka panjang AC adalah ....

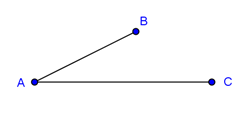
Penyelesaian:

Perhatikan bahwa AB : AC = 2 : 3 atau dapat dinyatakan sebagai ABAC=23$\frac{AB}{AC}=\frac{2}{3}$. Dengan demikian, diperoleh:

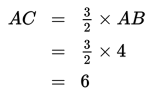
Jadi, panjang AC adalah 6 cm.

Contoh 2:

Pada ruas garis AB, terletak titik P di antara A dan B, sehingga AP : PB = 1 : 5. Jika panjang AB = 12 cm, maka panjang AP adalah...

Penyelesaian:

Diketahui titik P berada di antara A dan B, sehingga AB = AP + PB. Oleh karena AP : PB = 1 : 5, maka AB = AP + PB = 6 . Dengan demikian, AP : AB = 1 : 6 atau dapat dinyatakan sebagai APAB=16$\frac{AP}{AB}=\frac{1}{6}$. Dengan demikian, diperoleh:

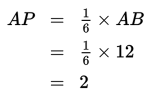
Jadi, panjang AP adalah 2 cm.

Contoh 3:

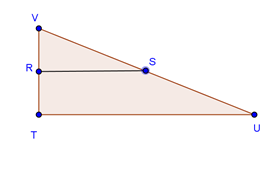
Pada gambar di atas, diketahui RS // TU. Jika UV = 9 cm, VT = 6 cm, VS = 3 cm dan UV : VS = VT : VR. Tentukan panjang VR.

Penyelesaian:

Berdasarkan informasi dari soal, diperoleh:

UV : VS = VT : VR

Dengan demikian, dapat ditulis menjadi UVVS=VTVR$\frac{UV}{VS}=\frac{VT}{VR}$. Dengan demikian, diperoleh:

Jadi, panjang VR adalah 2 cm.